Etapy tworzenia algorytmu
Co to jest algorytm?
Na algorytmice będziemy posługiwać się pojęciem algorytm. Cóż, to takiego? Myślę, że można powiedzieć, że jest to przepis jak z pewnych danych uzyskać określone wyniki.
Wbrew pozorom często stosujemy algorytmy w codziennym życiu. Przykładem może być przejście przez ulicę. Danymi są: ulica, ruch na niej oraz nasze położenie początkowe na krawężniku. Oczekiwanym wynikiem będzie znalezienie się po przeciwnej stronie ulicy. Algorytm (którego nauczono nas w dzieciństwie) mówi nam, jak tego dokonać. Można go zapisać w postaci tzw.łisty kroków:
- Spójrz w lewo.
- Jeśli samochód jest odpowiednio daleko przejdź do następnego punktu, w przeciwnym przypadku wróć do punktu 1.
- Spójrz w prawo.
- Jeśli samochód jest odpowiednio daleko przejdź do następnego punktu, w przeciwnym przypadku wróć do punktu 3.
- Spójrz włewo.
- Jeśli samochód jest odpowiednio daleko przejdź do następnego punktu, w przeciwnym przypadku wróć do punktu 5.
- Przejdź przez ulicę.
Oczywiście algorytm ten jest mocno uproszczony, w rzeczywistości punkt 7 powinien być bardziej rozbudowany (być może w połowie trzeba będzie się zatrzymać, cofnąć albo przyśpieszyć).
Algorytmy w kuchni
Typowymi przykładami z życia codziennego są przepisy kulinarne. Nazwa przepisu mówi o końcowym produkcie, natomiast na początku podane są niezbędne składniki oraz naczynia itp. Sam przepis jest algorytmem. Przypomnij sobie jak należy ugotować jajko na miękko. Przepis mówi, co należy zrobić, z czym i w jakiej kolejności.
Przykład algorytmu - przepis na pierniczki
Dane wejściowe:2 szklanki mąki; 2 łyżki miodu; 3/4 szklanki cukru; 1,5 łyżeczki sody oczyszczonej; 1/2 torebki przyprawy piernikowej; 1 łyżka masła; 1 jajko (+ dodatkowo 1 jajko do posmarowania); około 1/3 szklankiłekko ciepłego mleka.
Algorytm:
1. Mąkę przesiać na stolnicę, wlać rozpuszczony gorący miód i wymieszać (najlepiej nożem). Ciągle siekając, dodawać kolejno cukier, sodę, przyprawy, a gdy masałekko przestygnie - masło i jedno jajko.
2. Dolewając stopniowo (po 1 łyżce) mleka zagniatać ręką ciasto aż będzie średniotwarde i gęste (nie musimy wykorzystać całego mleka, bo masa może być za rzadka). Dokłladnie wyrabiać ręką, aż będzie gładkie, przez około 10 minut.
3. Na posypanej mąką stolnicy rozwałkować ciasto na placek o grubości maksymalnie 1 cm. Foremkami wykrajać z ciasta pierniczki, smarować rozmąconym jajkiem i układać na blasze wyłożonej papierem do pieczenia w odstępach około 2-3 cm od siebie (pierniczki troszkę podrosną).
4. Piec w piekarniku nagrzanym do 180 stopni przez około 15 minut. Przechowywać w szczelnie zamkniętym pojemniku, do 4 tygodni łub jeszcze dłużej. Pierniczki im są starsze tymłepsze. Z czasem też stają się bardziej miękkie.
5. Dekorować przed podaniem, najlepiej jak już będą miękkie. Do dekoracji można użyć samegołukrułubłukru wymieszanego z barwnikiem spożywczym. Zamiast barwnika spożywczego można użyć soku z granatułub z buraka. Pierniczki można dekorować roztopioną czekoladą i maczać w posypce cukrowejłub w wiórkach kokosowych.
Dane wyjściowe: Pyszne pierniczki
Algorytmy w matematyce
Z algorytmami miałeś do czynienia na matematyce. Typowym przykładem jest rozwiązanie równania kwadratowego. Dane w tym przypadku to współczynniki a, b, c równania ax2+bx+c=0, a wynikiem - pierwiastki, ewentualnie stwierdzenie, że nie ma takowych.
Przykład: Problem młodego Gaussa.
Szeroko znana jest historia Karola Gaussa, z którym miał problemy jego nauczyciel matematyki. Aby zająć czymś młodego chłopca, profesor kazał mu wyznaczyć sumę liczb a, a+1, a+2, ..., b, gdzie a,b∈N (jak głosi historia, było to a= 1 i b= 100). Zapewne nauczyciel pomyślał sobie, że tamten użyje algorytmu I i spędzi niemałą ilość czasu na rozwiązywaniu łamigłówki.Algorytm I wyznaczania sumy kolejnych liczb naturalnych
/ / W e j ś c i e :a,b∈N(a < b)
/ / W y j ś c i e :a+a+ 1 +...+b∈N
Niech suma, i∈N;
suma=0;
dla(i=a, a+ 1,...,b) suma=suma+i;
zwróć suma jako wynik;
Jednak że sprytny Gauss zauwa żył, żea+a+ 1 +···+b=a+b2(b−a+ 1). Dzięki temu wyznaczył wartość rozwiązania bardzo szybko korzystając z algorytmu II.
Algorytm II wyznaczania sumy kolejnychłiczb naturalnych
// W e j ś c i e : a,b∈N(a < b)
// W y j ś c i e : a+ a+1 + ...+ b∈N
niech suma∈N;
suma=((a+b)2)*(b−a+1);
zwróć suma jako wynik;
Zauważmy, że obydwa algorytmy rozwiązują poprawnie to samo zagadnienie. Mimo to inna jest liczba operacji arytmetycznych (+,−,∗,/) potrzebna do uzyskania oczekiwanego wyniku.
Poniższa tabelka zestawia tę miarę efektywności obydwu rozwiązań dla różnych danych wejściowych.
Zauważmy, że w przypadku pierwszego algorytmu liczba wykonywanych operacji dodawania jest równa(b−a+ 1)[instrukcja suma=suma+i]+(b−a)[dodawanie występuje tak że w pętli dla ... ].
Liczba operacji arytmetycznych potrzebna do znalezienia rozwiązania problemumłodego Gaussa.
| a | b | Alg. I | Alg. II |
| 1 | 10 | 19 | 5 |
| 1 | 100 | 199 | 5 |
| 1 | 1000 | 1999 | 5 |
Ciekawostka: Badaniem efektywności algorytmów zajmuje się dziedzina zwana analizą algorytmów. Czerpie ona obficie z wyników teoretycznych takich działów matematyki jak matematyka dyskretna czy rachunek prawdopodobieństwa.
Algorytmy w innych naukach
Także na innych przedmiotach mogłeś spotkać się z algorytmami. Na chemii uzyskiwałeś pewne związki chemiczne mając inne substancje orazłaboratorium. Na fizyce ważyłeś ciała stałe, a na biologii przygotowywałeś preparaty do oglądania ich pod mikroskopem.
Definicja algorytmu
We wszystkich tych przypadkach postępowałeś wg pewnej instrukcji, która od stanu początkowego prowadziła do stanu końcowego. Ten zestaw instrukcji wraz z stanem początkowym i efektem końcowym - od dzisiaj - będziemy nazywać algorytmem.
S. Węgrzyn algorytm definiuje w następujący sposób: „Przez algorytm będziemy rozumieć(…) skończony ciąg operacji wraz z ściśle sprecyzowanym porządkiem ich wykonywania, które po realizacji dają rozwiązanie dowolnego zadania z określonej klasy”
L. Banachowski i A. Kreczmar przyjmują, że: „Algorytmem nazywa się najczęściej przepis postępowania, który ma prowadzić w sposób autonomiczny do rozwiązania określonego zadania. Ten przepis postępowania powinien być na tyle precyzyjny, aby posługiwanie się nim polegało tylko na automatycznym wykonywaniu instrukcji tego zapisu. Zakłada się przy tym, że pewne pierwotne instrukcje tego przepisu są wykonalne, to znaczy, że są one zdefiniowane i w algorytmie nie musi się ich definiować, ale można ich używać”
Algorytm również określa się, jako ”dokładny przepis określanego zagadnienia, najczęściej przedstawiany w postaci skończonej sekwencji elementarnych (na danym poziomie) operacji, które należy wykonać”
Ćwiczenie
- Podaj kilka przykładów algorytmów z życia codziennego.
Specyfikacja problemu
Integralną częścią algorytmu jest jego specyfikacja, czyli co jest dane (Wejście), a co należy uzyskać (Wyjście).
Cechy algorytmów
--> poprawność - algorytm powinien zwracać poprawne wyniki, odzwierciedlające rzeczywistość
--> jednoznaczność - algorytm powinien przy takim samym zbiorze danych wejściowych zwracać takie same wyniki
--> skończoność dla każdego zbioru poprawnych danych wejsciowych algorytm powinien zwracać wyniki w skończonejłiczbie kroków
--> efektywność - algorytm powinien prowadzić do rozwiązania problemu w jak najmniejszejłiczbie kroków.
--> Uniwersalność - algorytmy operują na zmiennych a nie na konkretnychłiczbach

Specyfikacja
- Wejście: Stoimy na krawężniku
- Wyjście: Jesteśmy po przeciwnej stronie
Schemat blokowy
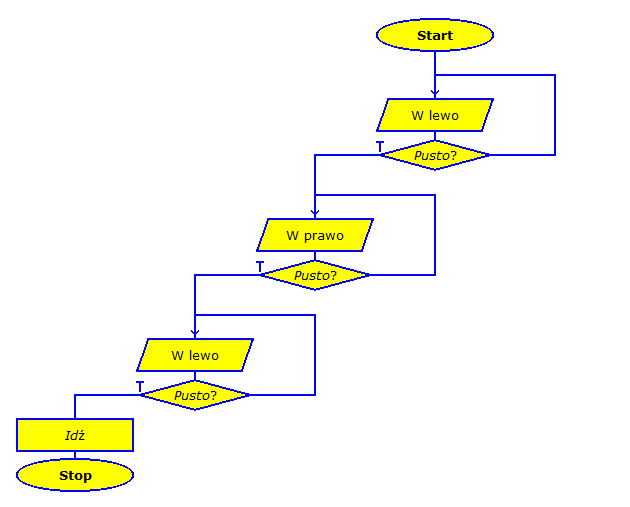
Jak widać taka prezentacja algorytmu jest bardziej czytelna i dlatego większość algorytmów będzie pokazana w tej postaci.
Skrzynki
|
Algorytm zaczyna się od tej skrzynki. Musi wystąpić w schemacie dokładnie raz! |
|
| Algorytm kończy się tą skrzynką. Musi występować przynajmniej jeden raz. | |
| Skrzynka wejścia, czyli pobieranie danych od użytkownika. W podanym przykładzie dana zostanie zapisana w zmiennej x. Zamiast We: można użyć Podaj, Wpisz itp. |
|
| Skrzynka wyjścia, czyli wypisywanie wyników działania algorytmu. W podanym przykładzie dana zostanie wypisana wartość zmiennej x. Zamiast Wy: można użyć Wypisz, Wyświetl itp. |
|
| Skrzynka instrukcji. Tu realizowane są wszelkie obliczenia. W podanym przykładzie wartość zmiennej zwiększy się o 1. Znak := należy czytać staje się. |
|
| Skrzynka warunkowa. Tu następuje rozgałęzienie algorytmu w zależności odłogicznej wartości warunku. Jeśli jest prawdziwy algorytm pójdzie włewo (tam gdzie jestłitera T jak Takłub True), w przeciwnym przypadku uda się w prawo. |
Pozostałe symbole tworzą stanowią drogi, które łączą skrzynki. W niektórych sytuacjach dodatkowe strzałki precyzują kierunek ruchu.
- Stwórz algorytm obliczający pole trójkąta.
- Stwórz algorytm obliczający pole trapezu.
- Stwórz algorytm obliczający pole koła.
- Stwórz algorytm obliczający długość przeciwprostokątnej w trójkącie prostokątnym.
Wróć do spisu tematów