Algorytmy z warunkami.
Złożoność obliczeniowa to dziedzina informatyki teoretycznej zajmująca się klasyfikacją języków formalnych ze względu na ilość zasobu — czasu i pamięci — potrzebnego do rozpoznawania języka. Ponieważ język formalny jest abstrakcyjnym odpowiednikiem problemu algorytmicznego, teoria ta dostarcza narzędzi do szacowania trudności obliczeniowej takich problemów. Niniejszy kurs zapoznaje uczestników z najważniejszymi rezultatami badań dotyczącymi klas złożoności, ich własności i wzajemnych zależności a także omawia wynikające z tych faktów wnioski dotyczące praktycznych problemów algorytmicznych.
Złożoność obliczeniową przedstawiamy jako funkcję, której argumentem jest rozmiar danych wejściowych algorytmu,
zaś wartością jest:
--> liczba operacji (dla złożoności czasowej)
--> liczba bajtów czy zmiennych typów elementarnych (dla złożoności pamięciowej).
Operacje elementarne to: instrukcje warunkowe, przypisania i operacje arytmetycznych i logiczne itp.
Złożoność pamięciowa to ilość pamięci wykorzystanej w celu realizacji algorytmu, wyrażana w liczbie bajtów lub liczbie zmiennych typów elementarnych.
Złożoność czasowa to czas wykonania algorytmu wyrażany zazwyczaj w liczbie operacji elementarnych.
Rozróżniamy dwa rodzaje czasowej i pamięciowej złożoności obliczeniowej:
--> pesymistyczna złożoność obliczeniowa dotyczy najgorszego przypadku zestawu danych, zatem określa ona największą ilość operacji dominujących (lub komórek pamięci), która może być wymagana dla najgorszego przypadku n danych wejściowych.
--> oczekiwana złożoność obliczeniowa dotyczy typowego zestawu danych i określa statystycznie średnią ilość operacji dominujących (komórek pamięci), które należy wykonać dla typowego zestawu danych, aby rozwiązać problem.
szybkość komputerów oraz złożonośc obliczeniowa
Przy konstruowaniu algorytmów często sięgamy do matematyki. Kolejne liczby naturalne tworzą ciąg arytmetyczny:
a1 = 1, d = 1
a2 = a1 + d = 1 + 1 = 2
a3 = a1 + 2d = 1 + 2 = 3
a4 = a1 + 3d = 1 + 3 = 4
...
an = a1 + (n - 1)d = 1 + n - 1 =
n
Dla ciągu arytmetycznego suma n kolejnych wyrazów wyraża się wzorem:
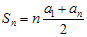
W naszym ciągu mamy:
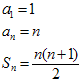
Zatem algorytm można uprościć do postaci:
Lista kroków z czasami wykonania operacji:
| Krok | Operacja | Czas wykonania |
| Krok 1: | Czytaj n | t1 |
| Krok 2: | suma ← n(n + 1)/2 | t2 |
| Krok 3: | Pisz suma | t3 |
| Krok 4: | Zakończ | t4 |
T(n) = t1 + t2 + t3 + t4, niech ta = t1 + t2 + t3 + t4
T(n) = ta - stały czas wykonania
Czas wykonania tego algorytmu nie zależy od wartości n, czyli jest stały. Taki wynik jest o niebo lepszy od poprzedniego. Wniosek: często opłaca się rozważyć dany problem matematycznie.
Klasy złożoności
Przy analizie algorytmów korzysta się z tzw. klas złożoności obliczeniowej (ang. computational complexity class), które określają rząd funkcji T(n). Jednym ze sposobów określania rzędu tej funkcji jest popularna notacja omikron (zwana także notacją dużego O) o następującej definicji:
Mówimy, że T(n) = O(f(n)) (funkcja złożoności obliczeniowej T(n) jest rzędu funkcji f(n)) jeśli potrafimy znaleźć takie n0 ∈ N oraz takie c ∈ R, iż dla każdego n ≥ n0 prawdziwa jest nierówność:
T(n) ≤ cf(n)
Przykład:
Funkcja złożoności obliczeniowej wyraża się wzorem
T(n) = 5n - 4
Udowodnimy, iż T(n) = O(n). W tym celu musimy wskazać takie n0 i takie c, aby dla każdego n większego od n0 spełniona była nierówność:
5n - 4 ≤ cn
Wystarczy przyjąć:
n0 = 1
c = 5
Wtedy 5n - 4 < 5n, co jest spełnione dla wszystkich n ≥ 1. Udowodniliśmy w ten sposób, iż T(n) = O(n).
Przykład:
Funkcja złożoności obliczeniowej T(n) = 3n2 + 5n - 3. Należy wykazać, iż T(n) = O(n2).
Przyjmujemy n0 = 1 i c = 5. Wtedy, zgodnie z definicją notacji omikron, otrzymamy nierówność:
3n2 + 5n - 3 ≤ 5n2
Sprawdzamy, czy jest spełniona dla n ≥ n0.
Dla n = 1: 3n2 + 5n - 3 = 3 +
5 - 3 = 5 ≤ 5n2 = 5 - spełnione
Dla n = 2: 3n2 + 5n - 3 = 12 + 10 - 3 = 19 ≤ 5n2
= 20 - spełnione
Dla n = 3: 3n2 + 5n - 3 = 27 + 15 - 3 =
39 ≤ 5n2
= 45 - spełnione
Dla n = 4: 3n2 + 5n - 3 = 48 + 20 - 3 = 65 ≤ 5n2
= 80 - spełnione
...
Przy wzroście n lewa strona nierówności rośnie wolniej od prawej, zatem nierówność będzie spełniona dla każdego n ≥ n0. Wykazaliśmy, że T(n) = O(n2).
Klasę złożoności obliczeniowej algorytmu można rozpoznać niekiedy po jego cechach charakterystycznych:
O(1) - stała klasa czasowej złożoności obliczeniowej
Algorytm wykonuje stałą liczbę operacji bez względu na rozmiar danych n.
O(n) - liniowa klasa czasowej złożoności obliczeniowej
Algorytm wykonuje stałą liczbę operacji dla każdej danej n.
O(n2) - kwadratowa klasa czasowej złożoności obliczeniowej
Dla każdej danej n algorytm wykonuje proporcjonalną do n liczbę operacji.
Oprócz powyższych istnieją również inne charakterystyczne klasy złożoności obliczeniowej, o których dowiesz się w dalszej części kursu informatyki (O(log n) - logarytmiczna, O(n log n) - liniowo logarytmiczna, O(2n) O(n!) - wykładnicza).
Klasy pamięciowej złożoności obliczeniowej określamy podobnie, w zależności od liczby zajętych przez algorytm komórek pamięci:
O(1) - stała klasa pamięciowej złożoności obliczeniowej
Algorytm zużywa stałą liczbę komórek pamięci bez względu na rozmiar danych n.
O(n) - liniowa klasa pamięciowej złożoności obliczeniowej
Algorytm zużywa liczbę komórek pamięci proporcjonalną do n.
O(n2) - kwadratowa klasa pamięciowej złożoności obliczeniowej
Dla każdej danej n algorytm zużywa liczbę komórek pamięci proporcjonalną do n.
Podobnie jak złożoność obliczeniowa, klasa złożoności obliczeniowej może być optymistyczna, typowa lub pesymistyczna.
Znajomość klas złożoności obliczeniowej czasowej i pamięciowej dla różnych algorytmów pozwala informatykowi przewidywać zachowanie się tych algorytmów dla różnych zestawów danych oraz dobierać algorytmy dla określonych sytuacji. Dlatego jest to jedno z kluczowych pojęć algorytmiki.
W oszacowaniach posługujemy się ogólnie przyjętymi symbolami opisującymi złożoność obliczeniową:
◦ notacja Ο (dużego O) wprowadzona przez P. Bachmanna w 1894r - złożomość pesymistyczna;
◦ notacja Ω (omega) - złożonośc optymistyczna;
◦ notacja Θ (theta) - złożonośc średnia
Często stosowane złożoności:
log(n) – złożoność logarytmiczna
n – złożoność liniowa
n log(n) – złożoność liniowo-logarytmiczna
nk – złożoność wielomianowa
2n – złożoność wykładnicza
Przykłady
1. Szukamy elementu x na liście o długości N.
Dane wejściowe: lista + element do wyszukania.
Algorytm 1
Krok 1. weź pierwszy element listy;
Krok 2. wykonuj dopóki nie osiągniesz końca listy:
Krok 3. sprawdź czy bieżący element jest tym szukanym;
Krok 4. sprawdź czy osiągnąłeś koniec listy;
Krok 5. weź następny element z listy
Krok 6. Zakończ algorytm
Jeśli operacją elementarną jest sprawdź, O(N)=2N - złożonośc liniowa (w teorii O(n)=n).
--> Nieprawdą jest, że komputery są tak szybkie, że czas nie stanowi problemu (np. rozkład na czynniki pierwsze dużych liczb - 300 cyfr wymaga wielu lat).
--> Nieprawdą jest, że komputery w przyszłości staną się wystarczająco szybkie aby obliczać wszystkie problemy algorytmiczne.
--> Stale pojawia się potrzeba rozwiązywanie coraz większych problemów algorytmicznych.
Morał: Złożoność czasowa decyduje o tym czy dany algorytm jest przydatny.
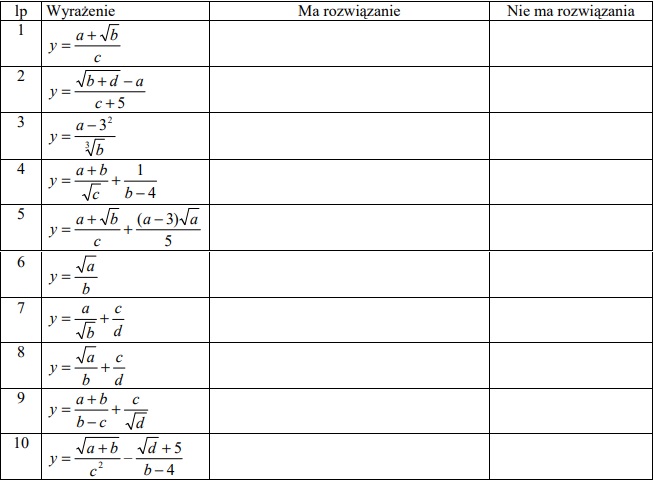
Zadanie 1
Wpisz w kolumnie nr 3 wyrażenie warunkowe określające kiedy dane równanie ma rozwiązanie
a w kolumnie nr 4 kiedy nie ma rozwiązania.
Zadanie 2
Napisz specyfikację do zadania oraz algorytmy rozwiązania w postaci pseudokodu, listy kroków oraz schematu blokowego, do problemu polegającego na wczytaniu z klawiatury
wartości dwóch zmiennych oraz wyświetleniu na ekranie tekstu informującego czy pierwsza liczba jest
podzielna przez drugą.
Zadanie 3
Napisz specyfikację do zadania oraz algorytmy rozwiązania w postaci pseudokodu, listy kroków oraz schematu blokowego, do problemu polegającego na wczytaniu z klawiatury
wartości zmiennej i wyświetleniu na ekranie tekstu informującego czy dana liczba jest ujemna, dodatnia
czy równa zeru.
Zadanie 4
Napisz specyfikację do zadania oraz algorytmy rozwiązania w postaci pseudokodu, listy kroków oraz schematu blokowego, do problemu polegającego na wczytaniu z klawiatury
wartości dwóch różnych liczb całkowitych a następnie wyświetleniu na ekranie większej z nich
Zadanie 5
Napisz specyfikację do zadania oraz algorytmy rozwiązania w postaci pseudokodu, listy kroków oraz schematu blokowego, do problemu polegającego na wczytaniu z klawiatury
wartości trzech różnych liczb całkowitych a następnie wyświetleniu ich na ekranie w kolejności malejącej
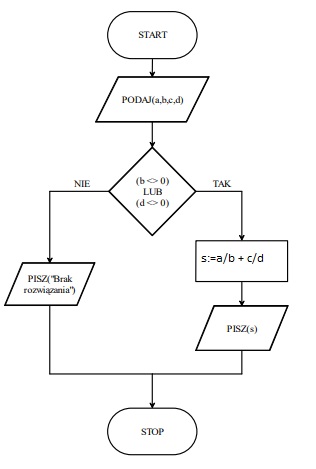
Zadanie 6
Poniżej przedstawiono dwa schematy blokowe. Wskaż błąd w każdym z nich i zapisz do nich treść zadania.
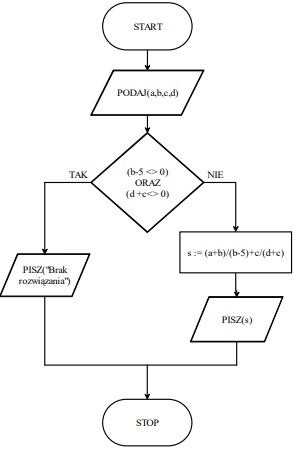
Zadanie 7
Wyznacz czasową złożoność obliczeniową oraz klasę czasowej złożoności obliczeniowej dla następującego algorytmu:
Wejście:
n - ilość liczb w tablicy
T[ ] - tablica zawierająca n liczb
Wyjście:
s - wynik pracy algorytmu
Dane pomocnicze:
i,j - indeksy elementów
| Krok 1: | s ← 0 |
| Krok 2: | i ← 0 |
| Krok 3: | Jeśli i = n - 10, to zakończ |
| Krok 4: | j ← 0 |
| Krok 5: | Jeśli j = 10, to idź do kroku 9 |
| Krok 6: | s ← s + T[i + j] |
| Krok 7: | j ← j + 1 |
| Krok 8: | Idź do kroku 5 |
| Krok 9: | i ← i + 1 |
| Krok 10: | Idź do kroku 3 |
Wróć do spisu tematów